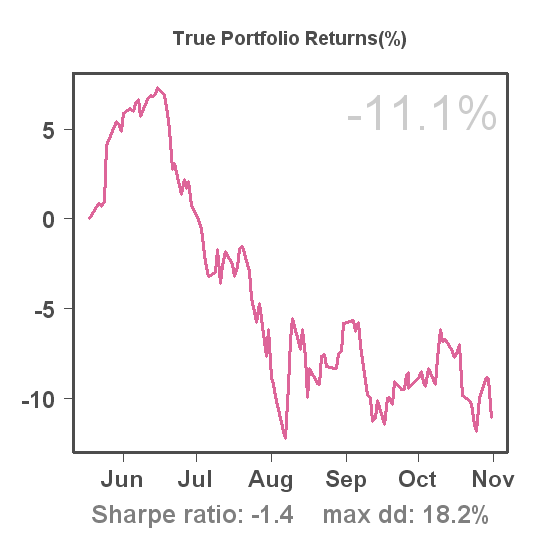
New hedge
The current put options on the Russell 2000 ETF (IWM) will expire in 2 weeks, so it's time to roll them forward. Therefore I sold (closed) the IWM Nov 72 puts today for $0.16 and bought (opened) the IWM Jan 72 puts for $1.26.
A series of notes related to trading of systems offered by 3rd party vendors
The current put options on the Russell 2000 ETF (IWM) will expire in 2 weeks, so it's time to roll them forward. Therefore I sold (closed) the IWM Nov 72 puts today for $0.16 and bought (opened) the IWM Jan 72 puts for $1.26.
Posted by
Science Trader
at
7:01 AM
0
comments
![]()
Starting this Monday, the optimal portfolio weights (for newly initiated positions) will change. Previous optimal weights were:
Weekend Trader: 32%
Trend Plays #1: 53%
ARS: 68%
Starting next week, the new weights will be:
Weekend Trader: 60%
Trend Plays #1: 49%
ARS: 41%
Since the weights sum to 150%, leverage will be about 1.5:1.
Posted by
Science Trader
at
12:15 AM
1 comments
![]()
Today, a limit was hit for a WYY position held by Trend Plays #1. Initiated on 6/4/2007, the trade yielded a nice 17% return.
Posted by
Science Trader
at
12:05 AM
0
comments
![]()
I ended my previous post with the words "Why is all this useful?", and today I'll try to answer this question.
Remember, I started discussing these distributions because Weekend Trader recently closed two trades with very large returns. Together with a trade with even larger returns (initiated in 2006) they have been responsible for almost half of the entire return (percentage-wise) of the system since its inception.
If you believe that these 3 trades are outliers, luck, the result of randomness etc, it would not make much sense to count on more of those for the future. After all, this is not about gambling but about trading. In that line of thinking, the performance of the system should be judged average at best.
However, if you believe these trades are an inherent part of the system's mechanics (perhaps due to a "let profits run" approach), the system (or vendor) should receive full credit for them, and performance might be judged good or even excellent.
The distributions we fitted can help to get more confidence in either the first ("luck") hypothesis or the second ("credibility") hypothesis, and allow us to determine how likely it is we can expect more of those big home-hitters in the future.
At first sight one might be tempted to conclude that since 3 out of 72 trades each resulted in increases on capital of more than 11%, the probability of this happening is 3/72 or 4.2%. I.e. we would expect every one out of 24 trades to increase equity by more than 11%. The problem with such an estimate is that it is not very precise: By the same calculation, the chance of observing a trade that increases equity by 10% (instead of 11%) is also 3/72, simply because none of the 72 trades so far showed a return between 10 and 11 percent. Similarly, the chance of observing a trade that increases equity with more than 12% (instead of 11%) falls quite abruptly to 1/72. Finally, if we would want to know the chance of a trade increasing equity by more than 17%, it would be zero, as we haven't seen those trades (yet)--but we all know that the chance is unlikely to be zero. Perhaps very small, but unlikely to be exactly zero.
Using distributions allow us to obtain more precise (and smoother) estimates. After fitting a distribution, we can get a precise estimate for whatever return percentage we are interested in, 10.4%, 10.8%, 200%, -30%, anything. It comes at a cost however: If we do a bad job at fitting a distribution, the probability estimate it will give us might be badly off. How badly? Consider the normal (Gaussian) distribution shown in red in the previous two graphs. Clearly it doesn't fit the histogram very well. According to this distribution, the chance of observing a trade that increases equity by more than 11% is only 0.27%! Compare this to the observed probability of 4.2%, and you see that this distribution underestimates the probability by a factor 15!
What do the other 3 fitted distributions have to say about the chance of observing a trade that increases equity by more than 11%?
- Cauchy: 3.7% (or 1 in 27 trades)
- Stable: 1.9% (or 1 in 53 trades)
- Generalized hyperbolic: 2% (or 1 in 48 trades)
These estimates look quite a bit more realistic than the Normal!
What about a trade that would increase equity by more than 20% (note: such a trade hasn't happened yet, so without fitting these distributions we wouldn't have a clue).
- Normal: 5.16e-08 (or 1 in 19,385,163 trades)
- Cauchy: 2% (or 1 in 51 trades)
- Stable: 0.7% (or 1 in 138 trades)
- Generalized hyperbolic: 0.5% (or 1 in 211 trades)
If we believe estimates from the last 3 distributions, such an event would not be that rare (the Normal estimate demonstrates once more how bad it is for fitting heavy-tailed distributions).
Based on these results, I have a hard time believing that these outlier trades are pure luck. I'm leaning more towards the second hypothesis: they're part of the characteristics of the system and should be treated as such. Obviously this doesn't mean it makes it a lot more comfortable to trade the system. It can be quite nerve-wracking to wait for the next big home-hitter... But analyses like these should give some confidence that it's worth waiting.
As you probably noticed, it can make quite a difference which distribution to choose... In subsequent posts I'll discuss how to measure and test how well a particular distribution fits the data, which might make such a choice a little easier.
Posted by
Science Trader
at
9:17 PM
0
comments
![]()
As we saw last week, the normal (Gausssian) distribution doesn't fit the returns per trade of Weekend Trader really well. Therefore I fitted 3 alternative distributions that have been suggested for modeling of financial data:
- Cauchy
- Stable
- Generalized Hyperbolic
I will discuss some of their properties in subsequent posts. Let's first see what they look like:
The y-axis now shows the density (rather than the frequency, shown in the previous post). Not surprisingly, the 3 alternative distributions seem to follow the histogram much closer than the normal (red line) distribution. I obtained the parameters of all distributions through maximum-likelihood estimation (mle), an often used optimization method in statistics.
Why is all this useful, you might ask? Hang on, we'll discuss soon...
Posted by
Science Trader
at
11:26 PM
3
comments
![]()
Today, Weekend Trader closed two positions for a very nice return, both about 46%. Because the system always initiates trades with 25% of equity (4 open positions at any point in time), the two positions combined added 23% to the equity of the system.
Obviously the question is, how often can we expect to celebrate such nice trades? And, what is the chance of even larger profits? And, finally, what are the chances the system will close a trade for a 46% loss.
Over the coming weeks I will attempt to address these questions, by looking into the distribution of the trade returns of some systems, including Weekend Trader. To kick it off, let's look at a histogram of the Weekend Trader returns per trade.
The total number of trades since inception was 72 and most (29) of them yielded between zero and 2% on equity (i.e. between zero and 8% on the trade itself). The small bar at the far right represents a trade with a return of 16.7% on equity (66% on the trade itself) on a position in TFR held during the first half of 2006. The next bar (counting from the right) represents the two recently closed trades I described earlier.
The average of the return on equity (i.e. the expected return in statistics lingo) is 1.15% and the standard deviation is 3.54%. As a comparison, I plotted the normal distribution with this mean and standard deviation (red line). Visual inspection shows that the Weekend Trader returns are not normally distributed, as the peak is higher and the tails are heavier. This is confirmed by the 3rd and 4th moments of the distribution, i.e. the returns have a skewness of 1.85 and kurtosis of 5.29, while both are zero for the normal distribution.
Why is it important to note that the returns are not normally (Gaussian) distributed? Well, if they were, we could predict the probability and size of extreme returns quite easily. For example, we could predict that 95% of the returns fall within a range of ~2 standard deviations below and above the mean. However, if the returns are not normally distributed, such predictions can be misleading and (in this case) underestimate the chance of an extreme (positive or negative) return.
What I appreciate a lot in these returns, is that the extreme values all appear on the positive end of the distribution (and of course, I like extremely large returns). On the negative end, the bars of the histogram are all lying below the normal distribution, which is very good.
Posted by
Science Trader
at
9:41 PM
2
comments
![]()
Earlier this week, I looked at 100-day rolling correlations between ARS and Weekend Trader, and between ARS and Trend Plays #1. This leaves one more combination for today: the correlation between Weekend Trader and Trend Plays #1:
This looks much more pleasant than the previous two graphs. For the most recent 100 trading days, the correlation between Weekend Trader and Trend Plays #1 is 0.26, which is only half of the correlation (0.52) between ARS and Trend Plays #1 for that same period. The max 100-day correlation between Weekend Trader and Trend Plays #1 is also quite reasonable: 0.37, substantially lower than the max 100-day correlation between Weekend Trader and ARS (0.62).
Posted by
Science Trader
at
9:38 PM
0
comments
![]()
Yesterday, I looked at 100-day rolling correlations between ARS and Weekend Trader. Today, I'll show the same for ARS and Trend Plays #1:
The correlation between ARS and Trend Plays #1 for the last 100 trading days is higher (0.52) than the correlation between ARS and Weekend Trader (0.42). The upward trend that started about a year ago is still continuing.
Posted by
Science Trader
at
9:31 PM
3
comments
![]()
One of the reasons to trade a portfolio of systems (like I do), is to reduce volatility. This works best if correlations between the systems are as close to zero as possible. It is interesting to track rolling correlations over time, and the figure below shows 100-day rolling correlations between ARS and Weekend Trader (red line), and a 95% confidence interval (blue lines, based on a simple bootstrap with 1,000 replications). See this post for a more detailed explanation.
The figure shows that for the most recent 100 trading days, the correlation between ARS and Weekend Trader was 0.42, down from a recent high at 0.62. I consider these numbers quite high--I'd prefer to have systems correlate less, because otherwise it doesn't matter much (from a volatility perspective) if I would trade only one system rather than multiple systems. So, I'll keep monitoring and hope it'll come down a bit in the next months.
Posted by
Science Trader
at
11:10 PM
0
comments
![]()