Weekend Trader Backtest

A while ago, I asked the vendor of Weekend Trader if any backtest data were available. Initially, he send me several graphs. More recently however I received the underlying data, so I could do some more analysis. I think this can be very valuable because we can compare the backtest results with the hypothetical C2 results and see if there's any evidence of massive overoptimization in the backtest (note the emphasis of massive; I think a little overoptimization is unavoidable and not a problem).

The figure below shows the hypothetical equity curve starting on 10/26/1999, which is the beginning of the backtest. After 1,508 trading days, the curve is no longer based on the backtested returns, but instead on the hypothetical C2 returns (starting October 24, 2005); the border between these different periods is marked by the dotted line. I have scaled the equity to an index, starting at 100; and included the S&P500 returns over the same period, also indexed at 100. The y-axis has a log-scale, which means that if the daily return percentage would be constant, the equity curve would follow a straight line.



Visual inspection seems to suggest that until so far the C2 results don't deviate much from the backtest. In fact, the first 250 days of the C2 history look very similar to the last 250 days of the backtest period, in terms of the slope of the curve. I will compare some other aspects (drawdowns, alpha, beta, sharpe etc.) in subsequent posts.

Trend Plays #1 Did it Again

Again, a Trend Plays #1 trade was closed for a really nice profit today:

TCHC bought 6/22/07 for $11.13, sold today for $14.51 = 30% profit

The profit is actually even larger, because I bought some more on 7/2/07 for $10.77 as a result of a portfolio re-allocation.

(click to enlarge...)


Note the 45% drawdown early may--it's real, not a split!

What Happened to Positive Forex?

Six weeks ago, I opened a demo account with BulldogFX and subscribed to Positive Forex.

I was very happy with the demo, and pleased to see that the demo auto trade fills matched hypothetical C2 fills almost exactly. However, I was less pleased with the performance of the system itself:



Every now and then systems are blowing up spectacularly on C2, and I'm very worried that I found myself close to subscribing to the system. Because I didn't finish my analysis of the system, I don't know what my final decision would have been...

On a positive note, I have always been very suspicious of forex systems relative to stock systems, because I have seen many forex systems blow up before. That's one of the reasons why I've only traded stock systems in my portfolio so far. Perhaps if there have been a few systems on C2 with stable track records of more than 2 years, I might consider forex again, but in the near future, I'll stick to stocks.

A possible explanation why Positive Forex blew up is that it was generating high returns by ignoring hidden risk (i.e. a collapse of the carry trade). You can find a nice explanation here.

New hedge

Yesterday, Weekend Trader replaced three of its four positions. It has now reached the target weight of 0.13, as discussed here. Because leverage is lower now, I needed to readjust the hedge. I also found that hedging with the Russell 2000 index tracker ETF (IWM) gives a slightly better fit than hedging with SPY.
Therefore, I sold the SPY Dec 142 puts for $6 (bought last week for $8.30) and bought the IWM Nov 72 put for $2.33.

ARS Excess Sharpe Ratio

Please find below the 100-day excess Sharpe ratio for ARS. See here for an explanation of the excess Sharpe ratio.

(click to enlarge...)


As the figure shows, ARS outperformed the SPY on a risk-adjusted basis for most of the 100-day rolling windows, although recently it substantially underperformed. Testing for difference between the Sharpe ratio of ARS and the Sharpe ratio of the SPY over the entire history (590 trading days), we find that it's not statistically different from zero, as the 95% confidence interval is [-0.58, 1.81].

Excess Sharpe Ratio

A reader pointed out an interesting problem with rolling alphas that I showed two weeks ago: When the model fit is bad (as shown by a low R-squared), the interpretation of alpha and beta is not very meaningful. In such cases, alpha typically has a very wide confidence interval and tracking alpha over time is of limited value or even misleading.

So, if we're not really interested in the relation between a system and an index because we think such a relation is rather weak or non-existent, we could instead compare the Sharpe ratio of the system to the Sharpe ratio of the index.

The figure below (upper panel) shows the 100-day rolling Sharpe ratio for Trend Plays #1 and the S&P 500. The difference between the two Sharpe ratios, which I call the system's excess Sharpe ratio, is shown in the lower panel. Most of the time the excess Sharpe ratio of Trend Plays #1 is greater than zero, i.e. the 100-day rolling Sharpe ratio of Trend Plays #1 is greater than the 100-day rolling Sharpe ratio of the S&P 500 index. In other words: The system does better than the index on a risk-adjusted basis.



The bad news is that the difference is not significantly different from zero (with 95% confidence) for any of the 100-day periods shown in the plot. Even when we construct a confidence interval for the difference between the Sharpe ratio of the system and the Sharpe ratio of the S&P using all 294 trading days, the difference is not significant: A bootstrapped confidence interval for the difference (with 10,000 replications, bias-corrected) shows [-0.886, 3.039].

Hedge Roll-over

I just changed the SPY put option hedge from the Dec 144 to the Dec 142 contract. This keeps the option delta such that the portfolio is approximately market-neutral. The Dec 144 contracts were purchased for $4.80 on July 31 and sold for $9.20 today. The Dec 142 contracts were bought for $8.30.

C2 still expanding

About six weeks ago, I posted a graph that showed the number of new systems launched on C2 for the past 30 days. The updated figure (as of today), looks like this:



It seems the current market volatility doesn't reduce the enthusiasm to launch new trading systems on C2. In fact, the number of newly launched systems (~220) has never been as high as last month.

Approximate Entropy

Many traders and investors prefer an equity curve as smooth as possible. It gives a sense of predictability, i.e. in our minds we extend the curve in the future and the smoother it is, the more confident we feel about our prediction. In many cases the Sharpe ratio is capable of summarizing the smoothness of the curve in a simple number, and the higher its absolute value, the smoother the curve.

Now, think about the Sharpe ratio of a sine wave for a moment...

Even though it's zero, we would be extremely happy to find a trading system with an equity curve represented by an exact sine wave. We would simply get into any open positions at the bottom of the wave and get out at the top, and repeat this over and over again for a huge profit.

Although this is an extreme example, it nicely shows that we might not only be interested in the smoothness of an equity curve, but also in the amount of randomness. I.e. it is possible that two systems have the same Sharpe ratios, while one system is less random than the other due to some much more subtle patterns not captured by the mean or standard deviation.

An interesting measure to quantify "randomness" in financial time series was published in the Proceedings of the National Academy of Sciences by Pincus and Kalman(*) about 3 years ago, based on a mathematical approach and formula called Approximate Entropy introduced in the early nineties by Pincus.

I won't go into all the details of this measure except for noting that it is rooted in the concept of information entropy developed by Shannon in 1948 as part of information theory (Wikipedia is a good first start for those who want to investigate further). Outside the world of finance, it has also found its application in the medical world (e.g. irregularity of heart rate). Approximate Entropy (ApEn) is a number, and the higher it is the more irregular (random) a time series. Thus, when applying ApEn to the daily returns of a C2 system, we would prefer a lower number over a higher number. ApEn requires 2 parameters: a block or run length (usually 1 or 2) and tolerance window (usually 20% of the standard deviation). In all figures below I use a block length of 1 and 20% of the standard deviation as tolerance windows, denoted as ApEn(1, 20% SD). The daily log-returns are used as inputs.

Over the entire history of a system, I got the following figures for the systems in my portfolio:
Trend Plays #1: 1.74
Weekend Trader: 1.95
ARS: 1.77

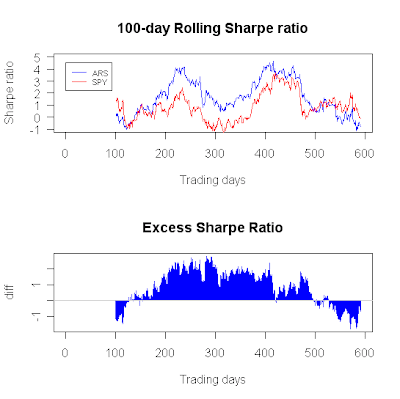
We can also do a rolling ApEn, estimated over 100 trading days:



This figure suggests that the equity curve of Trend Plays #1 has become more irregular (random) over time.



For Weekend Trader no such trend exists. Note that around the 400th trading day, ApEn was at its lowest point, suggesting relatively high regularity. This is reflected in the steady pattern of peaks and troughs in the equity curve during the preceding 100 trading days.



Finally, for ARS, we see yet a different curve. ApEn increased gradually over the past year, somewhat similar to what happened for Trend Plays #1.

These numbers and figures don't give an immediate clue how to improve returns and they also seem to be quite close across the systems. Pincus and Kalman show an example where a strong increase in ApEn preceded the Nov 1997 crash in the Hang Seng Index (HSI). I'll look for a C2 system that crashed and see if I can relate the crash to the system's ApEn in a future blog post.

(*) Pincus S, Kalman R E. Irregularity, volatility, risk, and financial market time series. Proceedings of the National Academy of Sciences 2004; 101(38): 13709-13714.

A few Words about the Drawdown

As you must have noticed, the portfolio drawdown gets larger on an almost daily basis, i.e. 17.8% from the peak, 11.8% from the day I started this blog, and 8.9% since I made a major change in the portfolio on July 23 (terminating auto trading and extreme-os, and including Longstoch-ST and ARS).

So, let's analyze what's going on:

1. About half of the 17.8% drawdown from the previous peak is due to a drawdown before the major portfolio change, and about half is due to a drawdown after that date. In other words, I experienced two consecutive drawdowns on 2 different portfolios.

2. All systems in the new portfolio, except Trend Plays #1, are setting fresh max drawdowns every day:
ARS -9.71%
Weekend Trader -15%
Longstoch-ST -13.44%
Note, however that these started earlier than July 23. Losses since July 23 are about 8% per system on average.

3. Because I was leveraged, these losses were bigger in my portfolio. At the same time I was partly hedged (only fully hedged beyond S&P500 drawdowns of ~7%), so ending up with a portfolio drawdown of 8.9% since July 23 is nothing unusual.

4. The next few days will be interesting. If the sell-off continues, I will become fully (delta) hedged (because the SPY Dec 144 puts will start to have delta's < -0.5) and I will start to roll these over to lower strikes (to avoid becoming over-hedged). On the other hand, if the market rallies we have to hope that the systems will keep outperforming the market (i.e. their returns should exceed the losses on the puts).

5. Experiencing this drawdown has many positive sides. First, we can see the systems perform during adverse market conditions. This will only benefit me, as it allows a more robust selection of systems in the future. Second, I have learned that it will probably pay off to spend some time on improving the hedge, e.g. estimate betas with more advanced models, backtest various hedging strategies and use of multiple indices.

Longstoch-ST confusion

Apparently my previous post on Longstoch-ST caused some confusion. It was not clear whether I was forced to close my positions because the system will be terminated by the vendor or whether this was my own decision. To clarify: I decided myself to close the open positions this morning at the open, while I could also have decided to keep them open and wait for the official signal from the vendor to close the positions, possibly at a later date.

I understand that the vendor is planning to blend Longstoch-ST signals with signals from one of his other systems on C2, and launch this as a new system.

New Portfolio Weights

The weights of the current portfolio positions (excl. Longstoch-ST) are as follows:
Weekend Trader: 55%
Trend Plays #1: 73%
ARS: 14%

The new optimal weights will be:
Weekend Trader: 13%
Trend Plays #1: 57%
ARS: 78%

This sums up to 148%, which means leverage will be about 1.5:1

It might take a while before the actual positions will reflect these weights as Weekend Trader and Trend Plays #1 can hold positions for several weeks.

Longstoch-ST termination

I just got a note from the vendor of Longstoch-ST that he is considering terminating the system in its current form due to the recent drawdown. This means I have decided to close any open positions tomorrow at the open and delete the system from my portfolio.

On the one hand it is very unfortunate that I had to digest the full drawdown because it just started after the first signal I received. On the other hand its effect could have been much worse if this was the only system I was trading, or if I did not have my positions hedged.

I think I should have taken the downward trend in its alpha much more seriously, as that has actually been a greater concern to me than the current drawdown (which seems to follow the sell-off in the broader market closely).

You might remember I had to terminate extreme-os during a drawdown last month because of technical problems. I think I solved that problem successfully by sticking to end-of-day systems (terminating auto trading). I now have to terminate another system during a drawdown because the vendor decided to change the course/terminate it. This is something that will be much harder to prevent in the future. In fact, it is likely that many systems will be terminated once a heavy drawdown occurs, as subscribers are probably all fleeing away and new subscribers will be hard to attract with a major drawdown on the record.

On the other hand, the declining alpha (see yesterday's post) should have given a clue that something was not ok, and I regret that I didn't do this analysis before I subscribed.

Longstoch-ST alpha and beta

We continue with rolling alpha and betas, and examine results for Longstoch-ST:



Similar to what we noticed for Weekend Trader yesterday, alpha shows a steady decline from 0.18% per day over the first 100 trading days, to -0.10% for the most recent 100 days. Contrary to Weekend Trader, beta has not been increasing but was fairly stable, fluctuating between 0.46 and 0.81.

A test for a linear trend in alpha showed that alpha has been declining with 0.00133 percentage point per day, which is quite a bit steeper than Weekend Trader. The decline is almost significantly different from zero at the 90% confidence level (p = 0.119).