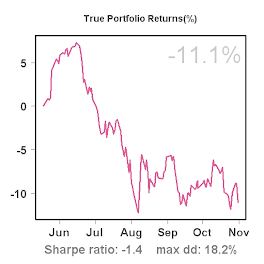
Longstoch-ST Sharpe ratio
The first thing I usually look for in a system is a high Sharpe ratio. It is reported, together with its confidence interval by C2:
Sharpe ratio = 2.2
95% CI [0.14 , 4.2]
To get an idea about these numbers we can compare them to the SPY (S&P 500 ETF), which could have been an alternative option for the same period:
Sharpe ratio = 1.5
95% CI [-0.6, 3.6]
The system does quite a bit better, I'd say!
Now, these are all estimates for a single point in time (today). Last month's estimate was likely different, and so will next month's estimate be. But as more observations (days) become available, we might expect these ratios to converge and the confidence interval to narrow. I like to watch this convergence over time, and hence I plot the value of the Sharpe ratio at each point in time, starting when the system is 100 days old (red line). I also plot the confidence interval, which I estimate with the bootstrap method (10,000 replications), using the percentile method (purple) and BCa (Bias-corrected and accelerated, green). I won't go into detail about the difference between the green and purple line, except for noting that the BCa (green) method is usually considered a superior estimate.
What we can see from the graph is that the Sharpe ratio was declining steadily from about 3 around day 100 to about 2 around day 200, and seems to have settled around 2 between days 200 and 250. Meanwhile the lower bound of the 95% confidence interval has been fluctuating between -0.5 and +0.5 with no clear trend.
All in all, I don't see any alarming patterns, and in an ideal scenario the Sharpe ratio would converge around 2 over time with the confidence interval narrowing further. This would also be close to the 5-year backtested results (2.14 Sharpe ratio) posted by the vendor on C2. I would consider a Sharpe ratio of 2 as quite good, and few end-of-day systems available on C2 show considerably higher Sharpe ratio over a similar or longer period.
One concern about using these bootstrap methods for confidence intervals is that they may be unreliable in case returns are autocorrelated. So to be sure, we check for autocorrelation, by plotting the correlation of the return at day t with the return at day (t-1), (t-2), ..., (t-12) and see if any of these lags are correlated. Results are shown below, and suggest that none of these correlations are significant (i.e. the bars stay within the horizontal bounds), which means that we can safely use these bootstrap methods for the Sharpe ratio confidence intervals.



1 comment:
scitra.blogspot.com is very informative. The article is very professionally written. I enjoy reading scitra.blogspot.com every day.
paydayloans payday
Post a Comment